Particle Settling in Water (II)#

Introduction#

In last computer lab, we studied the settling velocity of a sediment particle in water using several empirical equations. You probably have found out that it was not very convenient if we want to plot the settling velocity of a sand particle versus its diameter from micron to centimeter levels. In this lab, we will write our own settling velocity calculator for a sediment particle.

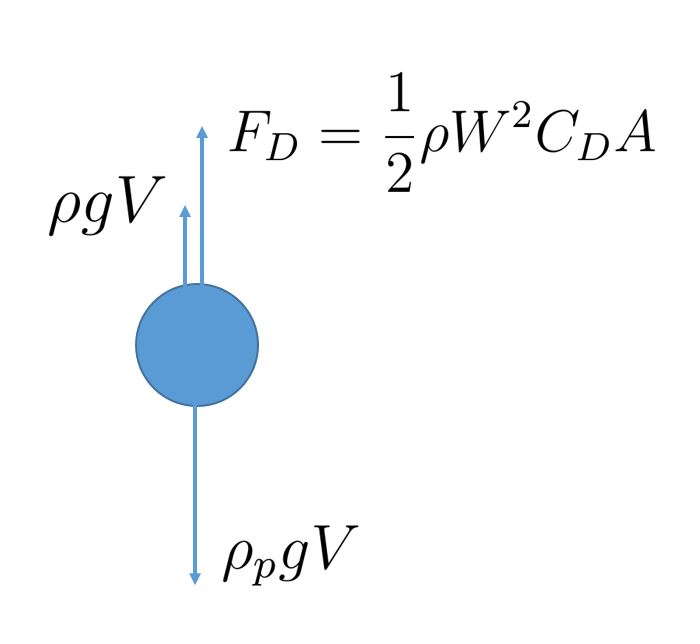
_images/diagram.jpg

Fig. 1 Free body diagram of a sediment particle settling in water.#

Theory#

From the previous lab, we have known that the equilibrium stage of a particle settling in the water can be balanced by gravitational force, buoyancy force, and drag force (see Fig. Fig. 1). Hence, we can easily derive:

(5)#\[W = \sqrt{\frac{2(\rho_p-\rho)gV}{\rho C_DA}}\]

Here, the drag coefficient \(C_D\) is a function of Reynolds number:

(6)#\[\begin{split}C_D = \begin{cases} \frac{24}{Re} & Re \le 1 \\ \frac{24}{Re}(1+0.15Re^{0.687}) & 1 < Re \le 1000 \\ 0.44 & Re>1000 \end{cases}\end{split}\]

where Reynolds number is \(Re = d_p W/\nu\) with \(\nu\) being kinematic viscosity of water.

In Eq. (5), you will find the settling velocity \(W\) appears on both sides of the equation. We will need solve for \(W\) using iterative approaches (with an initial guess value). “Scipy” is a Python library used for scientific computing and technical computing, which is very useful for engineers. I recommend that you use “fsolve” to solve the non-linear equation (5).

Hint

You might want to google from scipy.optimize import fsolve to find out how to use fsolve

Take-home work#

  1. Write your own settling velocity calculator to calculate the settling velocity of a sediment particle in water. Your function should take the following arguments: \(\rho_p\), \(d_p\), i.e,, density and diameter of the sediment.

Note

Use the following constant parameter in your calculator: water density \(\rho = 1000\) kg/m\(^3\); water viscosity \(\nu = 1\times10^{-6}\) m/s\(^2\). Assume spherical shape for all particles.

  1. Plot the setting velocity versus sediment diameter from 1 \(\mu\)m to 1 mm using your new calculator.

  2. Compare the plots of the velocity data using your previous codes for Equation (2) in Particle settling in water (I) along with today’s new plot.